PBRT 形体
本章介绍pbrt所用的诸如球、三角形等几何体素的抽象定义。在光线追踪器中,对一个清晰明了的系统设计而言,几何形体的精细的抽象定义是必不可少的关键部分,也是对面向对象方法的理想应用。所以几何体素都实现一个公共接口, 渲染器的其它部分只需使用这个接口,而不必关心相关形体的细节。这就把pbrt的几何子系统和着色子系统隔离开来。没有这个隔离,加入一个新形体就很困难,也容易出错。
pbrt把几何体素的细节隐藏在两重抽象之后。Shape类提供了对几何体素的基本几何性质的存取方法,比如求表面面积、包围盒,还有光线求交例程。Primitive类提供了额外的非几何的信息,比如材质。渲染器的其它部分只跟Primitive抽象接口打交道。本章主要介绍Shape类,Primitive接口会在第四章中介绍。
3.1 基本形体接口
Shape类使用了引用计数方法 — pbrt对每个形体都保持对其引用的计数,当计数为零时,该形体就被自动删除。虽然这个方法并非绝对有效,但这也是垃圾回收的一种方式,省去了对错误地释放形体的内存的担心。ReferenceCounted类实现了所有底层的相关机制(见A.2.2节)。
class COREDLL Shape : public ReferenceCounted {
public:
};
所有形体都是在物体坐标系中定义的。例如,所有球面的球心是物体坐标系的原点。为了把一个球面放置在场景中,必须提供从物体空间到世界空间的变换。Shape类存放变换的矩阵和它的逆阵。另外,Shape还有一个布尔参量:reverseOrientation, 用来决定是否反转表面法向量的方向。这一点很重要,因为法向量的方向常被用来决定形体的哪一侧是“外面”。例如,对于发光的形体而言,只有在法向量方向所指的一侧才发光。该参量可以由pbrt输入文件的ReverseOrintation语句说明。
Shape还存放对Transform::SwapsHandedness()调用的结果。每次找到光线交点时,该值要被用来构造DifferentialGeometry对象。所以,Shape构造器求出该值并存起来。
Shape::Shape(const Transform &o2w, bool ro)
: ObjectToWorld(o2w), WorldToObject(o2w.GetInverse()),
reverseOrientation(ro),
transformSwapsHandedness(o2w.SwapsHandedness()) {
}
const Transform ObjectToWorld, WorldToObject;
const bool reverseOrientation, transformSwapsHandedness;
3.1.1 求包围盒
每个形体都要实现求包围盒的函数,有两种函数:ObjectBound()返回形体在物体空间的包围盒,WorldBound()返回在世界空间的包围盒。第一个函数的实现由每个子类给出,而第二个函数有一个缺省的实现,即把物体空间中的包围盒变换到世界空间中并返回变换后的结果。如果形体很容易在世界空间中求得更紧密的包围盒(如三角形),就应该重写(override)该函数。
virtual BBox ObjectBound() const = 0;
virtual BBox WorldBound() const {
return ObjectToWorld(ObjectBound());
}
3.1.2 加细(Refinement)
并不是每个形体都能确定是否可以跟光线求交,例如,一个复杂的曲面先要细分成三角形才可以求交。还有可能一个形体只是用来代表存储在硬盘上的大量的形体的聚合。这时我们仅仅在内存中保留相应的几何信息文件和包围盒,只有当光线跟包围盒相交时,才把文件读到内存中。
Shape::CanIntersect()的缺省实现只返回真值,表示该形体“能”计算光线求交,所以那些不能求交的形体要重写该函数。
virtual bool CanIntersect() const { return true; }
如果形体不可以直接求光线交点,那么它必须提供Shape::Refine(),可以把形体分解成一组新的形体,其中有些形体可以直接求交,而另一些需进一步地加细。Shape::Refine()的缺省定义是发出一个错误信息,这样可以求交点的形体不必提供一个该函数的定义(因为父类已经提供了缺省的实现),pbrt保证当CanIntersect()返回真时,不会调用它。
virtual void Refine(vector
Servere(“Unimplemented Shape::Refine() method called.”);
}
3.1.3 求交
Shape类提供两个不同的求交例程。第一个是Shape::Intersect(), 它返回光线和形体的第一个交点的几何信息,其参数值落在光线的参数值范围[mint,maxt]之间。第二个是Shape::IntersectP(),它只返回交点是否存在,并不返回交点本身的任何细节。有些形体实现了非常高效的IntersectP()。
当我们读(或写)求交例程时,有几个非常重要的注意事项:
· 光线的结构包含了Ray::mint和Ray::maxt,它们定义了光线线段。求交例程必须忽略不属于这个范围的交点。
· 如果求到了交点,其沿光线的参数距离应该存放在传递给例程的参数指针tHit。如果有多个交点,只存最近的一个。
· 关于交点的信息存放在DifferentialGeometry结构中,该结构包括了表面在该点的局部几何性质,它在pbrt中被频繁地使用,并起着隔离几何部分和着色照明部分的作用。它的定义见第2.9节。
· 传到求交例程的光线是在世界空间定义的, 所以形体负责把光线变换到其物体空间做求交测试。所返回的DifferentialGeometry又是世界空间的。
Pbrt并没有把求交例程做成纯虚拟函数,而是在Shape类中提供了缺省实现(发出一条错误信息),所有那些Shape::CanIntersect()返回真的子类必须提供该函数的具体实现。
Virtual bool Intersect(const Ray &ray, float *tHit, DifferentialGeometry *dg) const {
Severe(“Unimplemented Shape: Interact() method called.”);
Return false;
}
Virtual bool IntersectP(const Ray &ray) const {
Severe(“Unimplemented Shape: InteractP() method called.”);
Return false;
}
3.1.4避免自相交
光线追踪过程中的一个经典问题是自相交问题:由于浮点计算的精度问题,当所追踪的光线离开前一个相交的表面时(例如阴影光线,镜面反射或折射等),下一个交点又落到了该表面。由于浮点精度的限制,所得到的交点可能稍稍处在表面之上或之下的位置。如果所追踪的新光线起始于该交点,那么有可能交点又落在该表面上(而实际情况是不存在交点)。
Pbrt解决这个问题所用的技巧是:把反射光线的Ray::mint设置成一个小epsilon值,但该值要足够大,从而在实际应用中的大多数情况下能够避免这个问题(见2.5节RAY_EPSILON的定义)。
不幸地是,不存在单一的一个常数能适应所有情况。该值要足够小,才能不漏掉可能的交点;又要足够大,可以避免自相交问题。对于任何一个常数,都会很容易地构造出自相交的场景。
3.1.5 着色几何信息
有些形体(特别是三角形网格)支持关于表面上点的两种类型的微分几何信息:真实的几何信息,它精确地反映表面的局部特性;还有着色几何信息,它可以有与真实微分几何不同的法向量和切向量。对于三角形网格而言,用户可以提供在网格顶点上的法向量和切向量,而三角形面上的点上的法向量和切向量是对顶点上的法向量和切向量进行插值得到的。
Shape::GetShadingGeometry()返回着色几何信息。缺省情况下,着色几何信息等同于真实的几何信息,所以缺省实现就是返回真实的几何信息。该函数的一个细微之处是可以传入一个物体到世界空间的变换;如果该例程需要从物体空间到世界空间的变换来计算着色几何信息,就必须使用该变换而不是Shape::ObjectToWorld变换。这样pbrt就可以实现物体的关联复制(object instancing),见4.1.2节。
virtual void GetShadingGeometry(const Transform &obj2world,
const DifferentialGeometry &dg,
DifferentialGeometry *dgShading) const {
*dgShading = dg;
}
3.1.6 表面面积
为了恰当地用Shape实现面光源,有必要计算一个形体在物体空间内的表面面积。跟求交函数一样,该函数也只用于那些可求交的形体。
virtual float Area() const {
Severe(“Unimplemented Shape::Area() method called.”);
return 0.0;
}
3.1.7 单面或双面(sidedness)
许多渲染系统,特别是那些基于扫描线或z缓冲器算法的系统,都支持“单面”的形体的概念,就是说,在形体前面看才是可见的,而从其后面看则看不到。特别是当几何体是封闭的,而观察点总是在它的外面的情况下,那些背对着观察者的部分就可以被剔除掉而不会影响最终的图像。这个优化可以加快这类隐藏面消除算法的速度。这个技术在光线追踪中则没有什么提高性能的可能性,因为常常在做背面测试(back-facing test)之前进行光线-物体求交运算。而且,如果单面物体不是封闭的,单面技术则会引起不一致的场景描述。例如,当追踪一条从光源到一个表面上点的阴影光线时,另一个表面可能遮挡住光源,而在另一个方向追踪阴影光线则不会遮挡。基于这些原因,pbrt不支持单面形体。
3.2 球面
class Sphere : public Shape {
public:
private:
}
球面是二次曲面的一种特殊形式。对于光线追踪程序来说,它是最简单的曲面,可以作为编制通用光线求交例程的良好开端。pbrt支持六种二次曲面: 球面,圆锥面,圆盘(一种特殊的圆锥面),圆柱面,双曲面和抛物面。
许多曲面可以用两种方式表达: 隐式和显式。描述三维曲面的隐式函数为:
f(x,y,z) = 0
所有满足上式的点(x,y,z)构成了这个曲面。对于球心在原点的单位球面来说,其隐式方程是x2+y2+z2-1 = 0。只有那些距离原点为单位长度的点才满足这一条件,所有这些点构成了单位球面。
还有许多曲面可以用参数化的方法来表达(即显式表达),即定义一个参数化方程,从2D点映射到曲面上的三维点。例如,一个半径为r的球面可以表达成2D球面坐标(θ,φ)的方程。其中θ的范围是0到π,φ的范围是0到2π。见图:
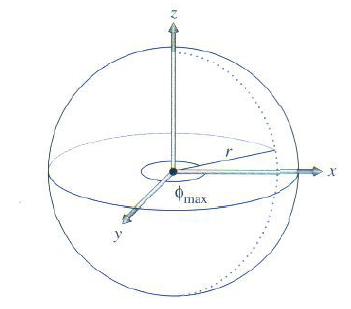
x = r sin θ cosφ
y = r sin θ sinφ
z = r cos θ
我们用下列的替换公式把该函数f(θ,φ) 变换成在区间[0,1] x [0,1]函数f(u,v):
Φ = uφmax
Θ = θmin + v(θmax – θmin)
这个形式非常有利于纹理映射, 因为我们可以很容易地把定义在[0,1]x[0,1]区间上的纹理映射到球面上。
在实现球面形体的过程中,显式方程和隐式方程都会用得上,这要取决于那一种最方便。
3.2.1 球面的构造
Sphere类在物体空间中定义了中心在原点的球面。为了把它放置在场景中,用户需要在输入文件中提供适当的变换。
球半径可以是任意的正值,球面有两个限定:首先,可以设定z值的最大值和最小值,超过或低于这个范围的部分就被截去了;再者,设定最大Φ值,球面从角度0扫到给定的Φmax, Φ值超出Φmax的那部分也被截去了。
Sphere::Sphere(const Transform &o2w, bool ro, float rad,
Float z0, float z1, float pm)
: Shape(o2w, ro) {
radius = rad;
zmin = Clamp(min(z0, z1), -radius, radius);
zmax = Clamp(max(z0, z1), -radius, radius);
thetaMin = acosf(zmin/radius);
thetaMax = acosf(zmax/radius);
phiMax = Radians(Clamp(pm, 0.0f, 360.f));
}
float radius;
float phiMax;
float zmin, zmax;
float thetaMin, thetaMax;
3.2.2 求包围盒
计算球面的包围盒还是很简单的。我们将用到用户提供的zmin和zmax。但是没有考虑Φmax < 2 π的情况(显然,如果考虑的话,会得到更紧密的包围盒)。
BBox Sphere::ObjectBound() const {
return BBox(Point(-radius, -radius, zmin),
Point(radius, radius, zmax));
}
3.2.3 求交点
因为在物体空间中球面中心在原点,求交点例程可以被简化。然而,如果球面已经被变换到世界空间上的另一个位置,就有必要把光线变换到物体空间中,然后再求交点。
bool Sphere::Intersect(const Ray &r, float *tHit, DifferentialGeometry *dg) const {
float phi;
Point phit;
return true;
}
首先,要把世界空间中的光线变换到球面的物体空间中,剩下的求交过程在物体空间中进行。
Ray ray;
WorldToObject(r, &ray);
中心在原点且半径为r的球面方程是:
x 2 + y2 + z2 – r2 = 0
将光线的参数方程(见第二章)代入上式,得:
(ox+tdx)2 + (oy+tdy)2 + (oz+tdz)2 – r2 = 0
这是一个关于t的二次方程,t值就是交点在光线上的参数位置。我们展开该式,并整理系数得:
A t2 + B t + C = 0
其中:
A = dx2 + dy2 + dz2
B = 2(dxox + dyoy + dzoz)
C = ox2 + oy2 + oz2 – r2.
用代码实现如下:
float A = ray.d.x*ray.d.x + ray.d.y*ray.d.y + ray.d.z*ray.d.z;
float B = 2 * (ray.d.x*ray.o.x + ray.d.y*ray.o.y + ray.d.z*ray.o.z);
float C = ray.o.x*ray.o.x + ray.o.y*ray.o.y + ray.o.z*ray.o.z – radius * radius;
该方程有两个可能的实数解:
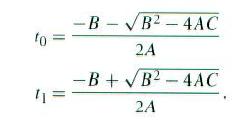
Quadratic()函数求解二次方程,如果没有实数解就返回false值,否则返回t0和t1.
float t0, t1;
if(!Quadratic(A, B, C, &t0, &t1))
return false;
inline bool Quadratic(float A, float B, float C, float *t0, float *t1) {
}
如果判别式(B2 – 4AC)为负值,则没有实根,光线和球面没有交点。
float discrim = B * B – 4.f * A * C;
if( discrim < 0. ) return false;
float rootDiscrim = sqrtf(discrim);
当B非常接近sqrt(B*B – 4AC)的正值或负值时,由于存在消去错误(cancellation error),常用的二次方程常常给出很差的数值精度。我们要用到下面更稳定的形式:
t0 = q / A, t1 = C/q
其中:
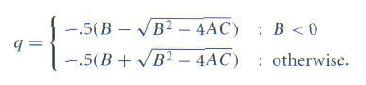
float q;
if( B < 0) q = -.5f * (B – rootDiscrim);
else q = -.5f * (B + rootDiscrim);
*t0 = q / A;
*t 1= C / q;
if ( * t0 > *t1) swap(*t0, *t1);
return true;
给定两个交点的t值,求交函数检查它们是否落在mint和maxt之间。由于我们保证t0 < t1(而mint < maxt),如果t0 > maxt或者t1 < mint,那么两个交点都不会在这个范围之中。否则的话,我们检查t0是否小于mint, 如果是,则忽略它再试t1。如果t1也不在范围之内,就不存在交点了。如果有交点的话,thit保存交点的参数距离。
if (t0 > ray.maxt || t1 < ray.mint)
return false;
float thit = t0;
if (t0 < ray.mint) {
thit = t1;
if (thit > ray.maxt) return false;
}
3.2.4 部分球面
得到光线和整球的交点后,还要考虑带有z和Φ的裁剪范围的部分球面的情况。处于被裁剪区域的交点要被舍去。首先,我们要计算交点在物体空间的位置phit和对应的Φ值。利用球面的参数形式,我们有:
y/x = (r sinθ sinΦ) / (r sinθ cosΦ) = tanΦ
故得Φ=arctan(y/x). 由于C标准函数atan2f返回值的范围是[-π, π], 所以要把结果值转换到0和2π之间(以符合我们对球面的定义)。
phit = ray (thit);
phi = atan2f(phit.y, phit.x);
if(phi < 0.0) phi += 2.f * M_PI;
现在我们可以用z和Φ的裁剪范围来测试t0和t1值的有效性了。如果t0无效,就接着测试t1。
if (phit.z < zmin || phit.z > zmax || phi > phiMax) {
if(thit == t1) return false;
if(t1 > ray.maxt) return false;
thit = t1;
if (phit.z < zmin || phit.z > zmax || phi > phiMax)
return false;
}
到了这里,我们可以确定光线打到了球面上,可以进行DifferentialGeometry的初始化了。根据前面计算出的交点的Φ值和球面的θ值范围,我们可以计算[0,1]范围内的u值和v值,它们分别是Φ和θ值从各自范围到[0,1]的映射值。然后就可以求得位置偏导数dp/du,dp/dv,和法向量偏导数dn/du, dn/dv.
float u = phi / phiMax;
float theta = acosf(phit.z / radius);
float v = (theta – thetaMin) / (thetaMax – thetaMin);
求解球面上的点的偏导数是微积分的一个小练习。我们给出dp/du的x分量的求法,其它分量的求法类似,这里略去了。
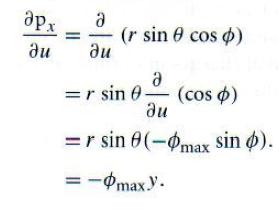
完整的结果如下:
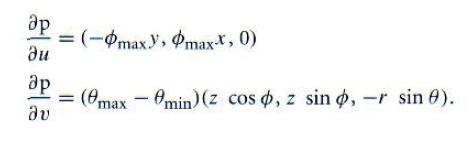
float zradius = sqrtf(phit.x * phit.x + phit.y * phit.y);
float invzradius = 1.f / zradius;
float cosphi = phit.x * invzradius;
float sinphi = phit.y * invzradius;
Vector dpdu(-phiMax * phit.y, phiMax * phit.x, 0);
Vector dpdv = (thetaMax – thetaMin) *
Vector(phit.z * cosphi, phit.z * sinphi,
-radius * sinf(thetaMin + v *(thetaMax – thetaMin)));
3.2.5 法向量的偏导数
掌握法向量沿表面u和v方向上的变化情况也是很有用的。例如,第11章所介绍的反走样技术就是使用这个信息,对映射到曲面上的纹理进行反走样。向量的微分变化dn/du,dn/dv由微分几何学中的Weingarten方程给出:

其中E, F和G是第一基本型的系数,分别如下:

利用前面求dp/du和dp/dv的方法,它们可以很容易地求得。e, f和g是第二基本型系数,分别为:
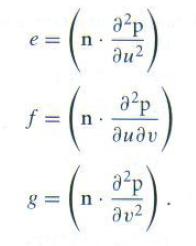
两个基本型跟曲面的局部曲率有基本的联系,可详见微分几何的教科书。求e,f,g需要计算二阶偏导数。对于球面而言,有下列二阶偏导数公式:
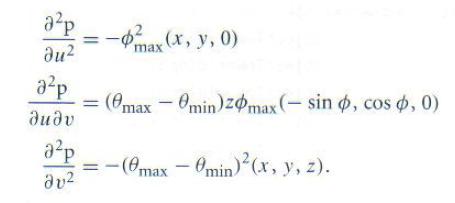
Vector d2Pduu = -phiMax * phiMax * Vector(phit.x, phit.y, 0);
Vector d2Pduv = (thetaMax – thetaMin) * phit.z * phiMax *
Vector(-sinphi, cosphi, 0.);
Vector d2Pdvv = -(thetaMax – thetaMin) * (thetaMax – thetaMin) *
Vector(phit.x, phit.y, phit.z);
< Compute coefficients for fundamental forms> =
float E = Dot(dpdu, dpdu);
float F = Dot(dpdu, dpdv);
float G = Dot(dpdv, dpdv);
Vector N = Cross(dpdu, dpdv);
float e = Dot(N, d2Pduu);
float f = Dot(N, d2Pduv);
float g = Dot(N, d2Pdvv);
float invEGF2 = 1.f / (E * G – F * F);
Vector dndu = (f * F – e * G) * invEGF2 * dpdu + (e * F – f * E) * invEGF2 * dpdv;
Vector dndv = (g* F – f * G) * invEGF2 * dpdu + (f * F – g * E) * invEGF2 * dpdv;
3.2.6 DifferentialGeometry初始化
计算好表面上点的参数值和相关的偏导数后,就可以用它们初始化关于该交点的DifferentialGeometry结构了:
*dg = DifferentialGeometry(ObjectToWorld(phit),
ObjectToWorld(dpdu),
ObjectToWorld(dpdv),
ObjectToWorld(dndu),
ObjectToWorld(dndv),
u,v,this);
因为找到了一个交点,参数tHit被更改成沿光线的交点参数距离(即变量thit的值)。如果潜在的交点比现存的交点距离更远,后续的求交测试就被免掉了。
到达了现在这一步,一个自然的问题是:世界空间到物体空间的变换对返回的参数距离有影响吗?我们知道,用来求交的光线经过平移、旋转、比例等变换从世界空间变换到物体空间。然而,可以证明在物体空间中的交点参数距离跟光线在世界空间求到的交点的参数距离完全相同。需要注意的是,如果光线在变换后被正规化了,上面的论断就不成立了。这也是不能对变换后的物体空间中的光线进行正规化的一个理由。
〈Update tHit for quadric intersection> =
*tHit = thit;
Sphere::InteractP()例程跟Sphere::Intersect()几乎相同,但它不会填写DifferentialGeometry结构。因为Intersect和IntersectP紧密相连,我们就不列出其它形体的IntersectP的实现了。
bool Sphere::IntersectP(const Ray &r) {
float phi;
float phit;
return true;
}
3.2.7 表面面积
为了计算二次曲面的表面面积,我们要用到一个标准的积分公式。如果定义曲线y = f(x) 在a到 b之间的一段绕x轴旋转,所生成的旋转曲面的面积是:
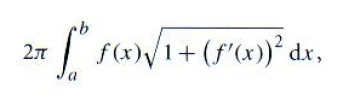
其中f'(x)是导数df/dx。对于部分的旋转曲面(旋转角度为Φmax), 则有:
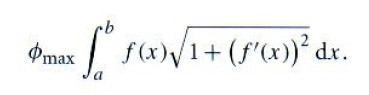
由于球面是关于一段圆弧的旋转曲面,定义圆弧的函数是:
f(x) = (r2 – x2)1/2
其导数为:
f'(x) = – x / (r2 – x2)1/2
由于球面的z值的裁剪范围是zmin ~ zmax,表面面积是:

对于整球,Φmax =2π,zmin = -r, zmax = r, 我们就用上式得到标准的球面面积公式: A = 4πr2,这也验证了公式的正确性。
float Sphere::Area() const {
return phiMax * radius * (zmax – zmin);
}
3.3 圆柱面
class Cylinder : public Shape {
public:
protected:
}
3.3.1 构造
另一个有用的二次曲面是圆柱面。pbrt提供了中心轴为z轴的圆柱面形体。用户要提供圆柱的最大z值和最小z值,半径,和扫过的最大Φ值。它可以用下面的等式表达:
Φ= u Φmax
x = r cosθ
y = r sinθ
z = zmin + v(zmax – zmin).
见图:

Cylinder::Cylinder(const Transform &o2w, bool ro, float rad,
float z0, float z1, float pm)
: Shape(o2w, ro) {
radius = rad;
zmin = min (z0, z1);
zmax = max (z0, z1);
phiMax = Radians(Clamp(pm, 0.0f, 360.0f));
}
float radius;
float zmin, zmax;
float phiMax;
3.3.2 求包围盒
和球面类似,求包围盒的算法只考虑了z值范围而没有考虑最大Φ值。
BBox Cylinder::ObjectBound() const {
Point p1 = Point(-radius, -radius, zmin);
Point p2 = Point(radius, radius, zmax);
return BBox(p1, p2);
}
3.3.3 求交
跟球面的情况类似,把光线方程代入圆柱面的隐式方程,就得到光线和圆柱面的求交公式。一个以z轴为中心轴且半径为r的无限长的圆柱面隐式方程是:
x2 + y2 -r 2 = 0
代入光线方程,得:
(ox + tdx)2 + (oy+tdy)2 = r2
将之展开,得到At2 + Bt + C二次方程系数如下:
A = dx2 + dy2
B = 2(dxox + dyoy)
C = ox2 + oy2 – r2
float A = ray.d.x * ray.d.x + ray.d.y * ray.d.y;
float B = 2 * (ray.d.x * ray.o.x + ray.d.y * ray.o.y);
float C = ray.o.x * ray.o.x + ray.o.y * ray.o.y – radius * radius;
对于所有二次曲面的形体而言,求解二次方程的过程是相似的,下面用到了许多在球面求交方法的许多片段:
bool Cylinder::Intersect(const Ray &r, float *tHit, DifferentialGeometry *dg) const {
float phi;
Point phit;
return true;
}
3.3.4 部分圆柱面
跟球面的情形一样,我们要用y的参数方程除以x的参数方程(得到tan Φ)来求Φ值。其结果也与球面的一致:
phit = ray(thit);
phi = atan2f(phit.y, phit.x);
if(phi < 0.) phi += 2.f * M_PI;
求交例程保证交点在给定的z值,Φ角度值也在给定范围值中。如果t0不满足的话,就要测试t1。
if(phit.z < zmin || phit.z > zmax || phi > phiMax ) {
if(thit == t1) return false;
thit = t1;
if(t1 > ray.maxt) return false;
if(phit.z < zmin || phit.z > zmax || phi > phiMax )
return false;
}
同样地,把Φ从范围[0, Φmax]变换到[0,1]之内得到u值,把z值从[zmin,zmax]变换到[0,1]得到v值。
float u = phi / phiMax;
float v = (phit.z – zmin) / (zmax – zmin);
关于圆柱面的偏导数很容易求得:
dp/du = ( -Φmaxy, Φmaxx, 0)
dp/dv = (0, 0, zmax – zmin)
Vector dpdu(-phiMax * phit.y, phiMax * phit.x, 0);
Vector dpdv(0, 0, zmax – zmin);
我们再用Weingarten方程求得关于圆柱面法向量的参数变化:
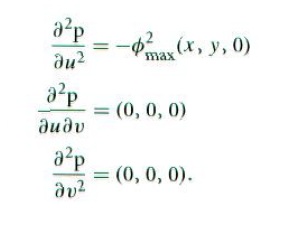
Vector d2Pduu = -phiMax * phiMax * Vector(phit.x, phit.y, 0);
Vector d2Pduv(0, 0, 0), d2Pdvv(0, 0, 0);
3.3.5 表面面积
圆柱面实际上就是卷起来的长方形。我们把这个长方形展开,其高为zmax – zmin, 其宽为r Φmax。
float Cylinder::Area() const {
return (zmax-zmin) * phiMax * radius;
}
3.4 圆盘(Disks)
class Disk : public Shape {
public:
private:
};
圆盘是一种有趣的二次曲面,因为它的求交例程简单直接,避免了求解二次方程。在pbrt中,Disk是在高度h上的半径为r的圆盘。用户可以指定最大Φ值。还可以指定一个内半径ri,其形状就变成了圆环。它可以用下面的参数形式表达:
Φ= u Φmax
x = ((1 – v) ri + vr) cosθ
y = ((1 – v) ri + vr)sinθ
z = h
见图:
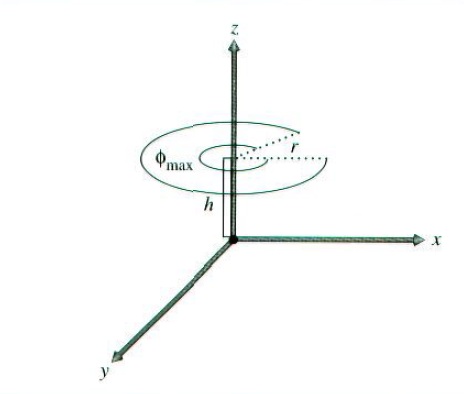
3.4.1 构造
Disk::Disk(const Transform &o2w, bool ro, float ht,
float r, float ri, float tmax)
: Shape(o2w, ro) {
hight = ht;
radius = r;
innerRadius = ri;
phiMax = Radians(Clamp(tmax, 0.0f, 360.f));
}
float height, radius, innerRadius, phiMax;
3.4.2 求包围盒
其过程很简单:
BBox Disk::ObjectBound() const {
return BBox (Point (-radius, -radius, height),
Point (radius, radius, height));
3.4.3 求交
求圆盘和光线交点也是很容易的。我们先求的光线跟圆盘所在平面z=h上的交点,然后测试交点是否在圆盘上。
return true;
}
第一步是计算光线跟圆盘所在平面交点的参数t 值。利用光线和包围盒求交的同样的方法,考虑光线在交点位置的z分量,它等于圆盘的高度,即:
h = oz + tdz
则有:
t = (h – oz) / dz
如果光线和圆盘平面平行(其方向的z分量为零),则没有交点。否则,我们检查t值是否在[mint,maxt]之间:
if(ray.d.z == 0) return false;
float thit = (height – ray.o.z) / ray.d.z;
if(thit < ray.mint || thit > ray.maxt)
return false;
如果交点phit到圆盘中心的距离大于Disk::radius或小于Disk::innerRadius,那么它就落在了圆盘之外。下面用到了优化措施:用距离平方进行比较,从而避免了求平方根运算:
Point phit = ray(thit);
float dist2 = phit.x * phit.x + phit.y * phit.y;
if (dist2 > radius * radius || dist2 < innerRadius * innerRadius)
return false;
如果交点通过了距离检查,最后的测试是看Φ值是否在0到Φmax之间。同其它形体一样,我们有:
flaot phi = atan2f(phit.y, phit.x);
if(phi < 0) phi += 2. * M_PI;
if(phi > phiMax)
return false;
求得交点后,需要变换Φ值到区间[0,1]计算出参数u值,并求v值。交点出的偏导数也可以用前面提到的方法求得。另外,dn/du, dn/dv都等于零,因为圆盘上的法向量都相同。
float u = phi / phiMax;
float v = 1.f – ((sqrtf(dist2) – innerRadius) / (radius – innerRadius));
Vector dpdu(-phiMax * phit.y, phiMax * phit.x, 0.);
Vector dpdv(-phit.x/(1-v), -phit.y/(1-v), 0.);
Vector dndu(0,0,0), dndv(0,0,0);
3.4.4 表面面积
圆盘面积很容易求得,因为这只是求部分圆环的面积:
A = Φmax(r2 – ri2) / 2
float Disk::Area() const {
return phiMax * 0.5f *
(radius * radius – innerRadius * innerRadius);
}
3.5 其它二次曲面
pbrt还支持其它三种二次曲面: 圆锥面, 抛物面,双曲面。这里不再讨论它们的具体实现,因为所有的方法都跟前面所提到了类似,这里只概括它们的隐式方程和参数形式。
3.5.1 圆锥面
假设以z轴为中心轴的圆锥面半径为r,高度为h,其隐式方程为:
(hx/r)2 + (hy/r)2 – (z-h)2 = 0
其参数形式为:
Φ= u Φmax
x = r(1 – v) cos Φ
y = r(1 – v) sin Φ
z = vh.
其偏导数为:
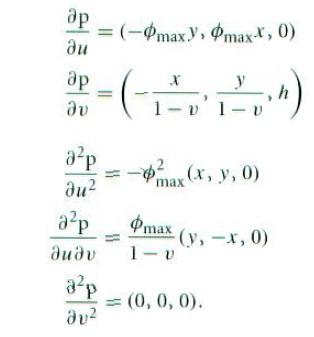
3.5.2 抛物面
假设以z轴为中心轴的抛物面半径为r,高度为h,其隐式方程为:
hx2/r2 + hy2/r2 – z = 0
其参数形式为:
Φ= u Φmax
z = v(zmax – zmin)
r = rmax(z/zmax)1/2
x = r cos Φ
y = r sin Φ
其偏导数为:
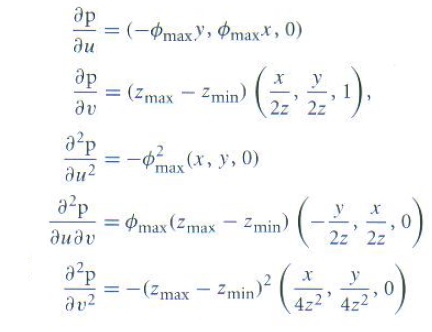
3.5.3 双曲面
双曲面其隐式方程为:
x2 + y2 – z2 = -1
其参数形式为:
Φ= u Φmax
xr = (1 – v) x1 + vx2
yr = (1 -v)y1 + vy2
x = xr cos Φ + yr sin Φ
x = xr sin Φ + yr cos Φ
z = (1 -v)z1 + vz2
其偏导数为:
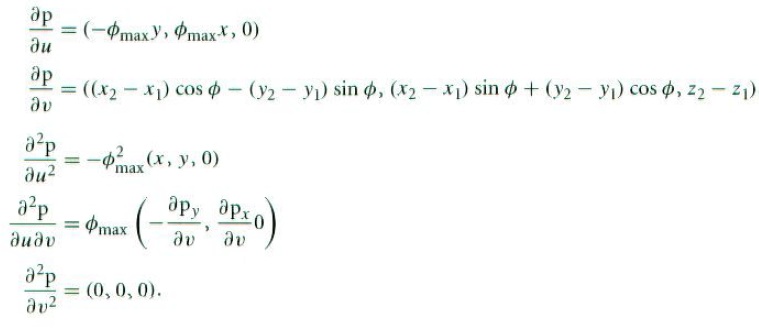
Categories: Garfield's Diary
