PBRT 具有照片真实感的渲染和光线追踪算法

1.2 具有照片真实感的渲染和光线追踪算法

具有照片真实感的渲染的目标就是所生成的图象如此真实,看上去和同一景物的相片难以区分.”难以区分”这一词并不准确,因为不同的观察者对同一图像的感知并不相同.但是在大多数情况下,我们会满足于对光和物质交互作用的精确模拟,这要依赖于我们对能生成”好”的图像的三维显示技术的理解.

大多数的具有照片真实感的渲染系统都基于光线追踪算法.光线追踪实际上是很简单的;在某一场景环境中,穿过场景的光线作用于物体并反射出去,而光线追踪算法就是跟着光线的路径跑的.

有许多方法写光线追踪程序, 所有这些程序至少要模拟以下的物体和现象:

1. 相机:景物是怎么被观察的,在哪里去观察?相机生成从观察点到景物的光线.

2. 光线和物体的求交:我们必须精确地知道光线在何处跟几何体相交.另外,我们需要知道物体在相交点处的某些性质,比如表面法向量.大多数光线追踪程序可以找到一条光线跟多个物体的交点,并返回最近的一个交点.

3. 光源分布:没有光源的照射,就没得可渲染的了.一个光线追踪程序必须建立关于光源在整个场景里的分布模型– 这不仅仅包括光源的位置,还包括它们是如何把能量分布于空间的.

4 可见性:为了得知一个光源是否在一个表面上的一点施加能量,我们必须知道从该点到光源是否有一条不被遮挡的路径.幸运地是,这并不难办到,因为我们可以在该点和光源之间建立光线,找到最近的光线/物体交点,并把交点处距离跟光源距离比较.(很显然, 交点处距离> 光源距离,或者根本就没有交点时,没有遮挡).

5.表面散射(Surface scattering):每个物体都应有对起外观的描述, 其中包括光源是如何跟其表面交互作用的, 光是如何散射的,等等, 通常我们只对直接散射到相机的那部分的光的性质感兴趣.表面散射模型通常是参数化的,这样才能模拟不同的物体外观.

6. 递归式光线追踪(Recursive ray tracing): 因为光可以碰撞到几个其它的表面后才到达一个表面, 所以有必要追踪额外的(起点于此表面的)光线来捕捉这个效果.这对象金属或玻璃这样的光滑表面而言非常重要.

7.光线传播(Ray propagation): 我们需要知道光沿着光线路径在空间中穿行时的情况. 如果整个场景是在真空中, 沿着路径上的光线的光能保持恒定不变.实际上更复杂的模型会考虑光线穿过雾,烟,和地球大气等等的情况.

1.2.1 相机

最简单的相机就是针孔相机.针孔相机有一个一端带有针孔的暗箱. 当针孔不被遮挡时,光线进入了这个小孔,打到位于暗箱另一端的感光纸上,经过足够的曝光时间而形成图像.虽然简单,但现在还有人在用呢,多半是艺术创作之用.

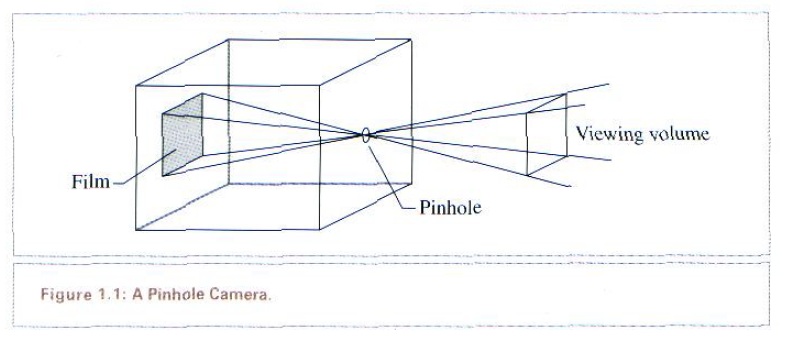
我们就从模拟针孔相机开始：图1.1表示了两个锥体：一个在相机之内，另一个在相机之外，我们能通过看到景物的景物必须在这个锥体之内，这个空间区域被称为“可视空间”（viewing volume).

（从图中我们可以想象在相机底片上的图像是应该上下颠倒的。）我们对这个相机模型做个如下改动：把底片板放在针孔之前，而跟针孔的距离保持不变。这是一个很方便的抽象方法。我们把针孔这个位置直接称为“眼睛”（eye)位置，

放底片板的垂直平面叫“近截面”（Near plane), 相对远处的地方放一个“远截面”（Far plane).这个四棱锥体就是相机所能观察到的范围。

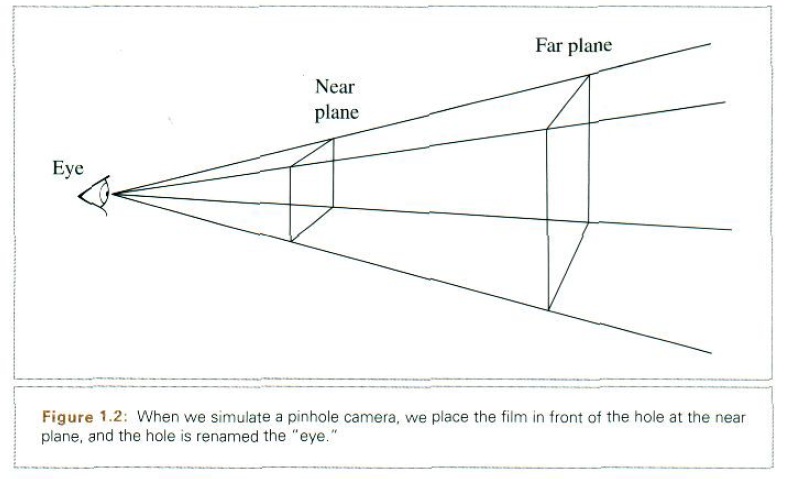
当我们用这个相机模型生成光线时，以近截面上的点（每个点对应所生成图像上的点）为原点，以从眼睛到该点的向量为光线的方向。

第六章会更详细地讨论pbrt所用的相机模型。

1.2.2 光线和物体求交

相机生成光线后，渲染器的第一个任务就是确定光线和哪一个物体先相交，以及在何处相交。这个交点就是沿着光线的可见点，这个点就是我们要费尽心机计算模拟光和该物体的交互作用的地方。为了找到这个点，我们必须测试光线和景物中的所有物体的相交情况，并选择那个最先相交的那个交点。给定一条光线r,其参数形式是:

    r(t) = o + t d
其中, o是光线的原点，d是其方向向量，t是参数，范围是[0，无穷大）。
如果物体的表面由隐函数 F(x, y, z)=0表示，那么光线跟表面的求交运算就很容易: 把光线方程代入隐函数中，得到关于t的方程。以球面为例：

球面隐函数是 x2 + y2 +z2- r2 = 0

代入光线方程得到：
    (Ox+t*dx)2+(Oy+t*dy)2+ (Oz+t*dz)2 – r2 = 0

这是一个关于t的二元一次方程。如果没有实根，则没有交点。如果有根，我们就选择那个较小的正值根。

只知道交点还不够，要对该点作着色运算，还需要该点上其它的几何性质，比如表面法向量。许多光线追踪程序只要表面法向量就够了，但对pbrt这样的更复杂的光线追踪程序，还需要表面的关于局部的偏导数值。

当然，大多数景物包含许多物体。强行地测试光线跟每个物体相交情况是很慢很慢的。一个优化方案是利用加速结构(acceleration structure)，可以快速地排除那些不相关的物体，使得算法时间优化成O(I log N）：I 是图像像素个数，N是物体个数。（建立加速结构的时间是O（N））。

我们在第三章描述几何求交的pbrt接口，在第四章描述加速结构。

1.2.3 光的分布

在光线/物体求交后，我们得到交点上的几何信息（位置，表面法向量，等）。回忆一下，我们的目标是得到光离开该点到达眼睛的光的能量。这需要了解光在场景中的几何分布和辐射分布。对于点光源而言，只需知道其光源位置就行了，而对于面光源（area light sources)，需要一个发光的几何体来表示这个面光源。在本节，我们只讨论点光源，更全面的光分布将在第5，13章中讨论。

[为方便起见，先补充几个关于光辐射的定义：
功率(power,又称辐射通量：radiantflux): 单位时间发出的辐射能。
辐射照度（Irradiance):单位面积上所接受的辐射功率。
辐射亮度（radiance：光源在于发射方向相垂直的单位面积上单位立体角内的辐射功率。
辐射照度E可写为：E=dΦ/dA,其中Φ是辐射通量， dA是包含该点的微分面积。]

假设有一个包含点光源（其辐射通量为Φ）的一个半径为r的球，其球面上辐射照度E是Φ/(4πr2).对于这样的包含点光源的两个大小不同的球而言，很明显地，在大球上的点的光能要小于在小球上的光能因为两个球都分布着同样的光能。这也很容易地得知，光的能量沿着光线路径以距离平方呈反比例地进行衰减。近一步地，如果微小表面片dA的法向量跟该点到光源的方向夹角是θ，
那么分布在dA上的光能和cosθ成比例。在dA上所分布的全部光能dE(微分辐射照度：differential irradiance)是：
        dE = Φcosθ /(4πr2).

那些已经熟悉计算机图形学中基本的光照知识的读者应该能从上式看到两条规律：光关于对倾斜面的cosine衰减，和距离平方的反比衰减。对场景中的多个光源的处理是很容易的：由于光照是线性的，每个光源的贡献值相叠加，就会得到所要求的结果。

1.2.4 可见性

前面介绍的光照分布忽略了一个很重要的要素：阴影。只有当光源到被着色的点的路径不被遮挡时，光源才能对该点提供照明。幸运地是，在光线追踪程序中，很容易确定光源到被着色点的路径被遮挡：只要在该点到光源建立一条光线。这种光线叫做阴影光线（shadow ray). 我们求得这条光线跟场景中所有物体的交点中最近的那个交点,并把交点到被着色点的距离跟被着色点到光源距离比较，如果前者大于后者（或者没有交点），则不存在遮挡，因而可判定光源对被着色点有光照作用。

1.2.5表面散射

为了对表面上的一点正确地着色,我们已有两个重要信息: 位置和入射光的光照信息.现在我们要确定入射光如何在表面上散射的. 特别是我们要知道沿着该点到达眼睛的那部分光的能量.

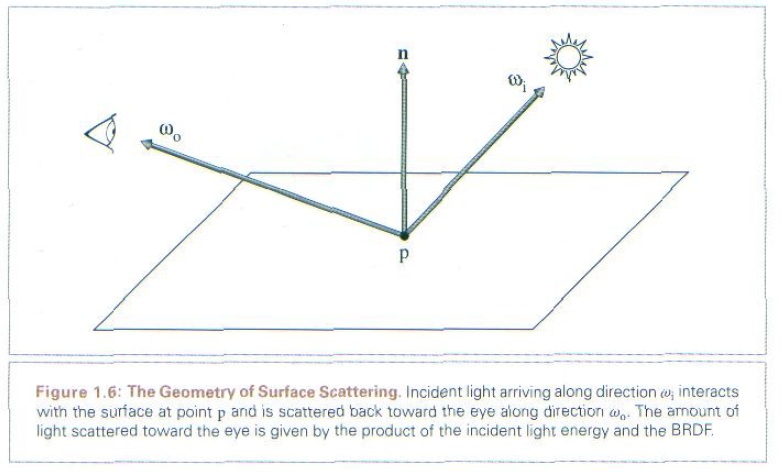
场景中每个物体都要提供描述表面上每个点的材质信息.这个描述可由双反射分布函数BRDF(Bidirectional Reflectance Distribution Function)给出.这个函数告诉我们给定入射方向ωi和出射方向ωo,有多少光能被反射出去. 记在点p的BRDF函数为fr(p, ωo,ωi).计算散射到眼睛的光能的方法如下:
  for each light:
               if light is not blocked:
                               incident_light = light.L(point)
                               amount_reflected =
                                               surface.BRDF(hit_point, light_vector, eye_vector)
                               L  += amount_reflected * incident_light

1.2.6 递归式光线追踪

Turner Whitted的关于光线追踪的论文强调了其递归性.比如说, 如果从眼睛起始的光线碰到象镜子这样的平滑物体, 我们要根据交点处的表面法向量来生成反射光, 并接着对该反射光线进行递归式追踪,以找到能到达镜面上点的光源,计算出它对原相机光线的光能贡献值.同样的技术可用于穿过透明物体的透射光线.  早期的光线追踪的论文热衷于炫耀那些包含镜子和玻璃球的图像, 因为其它的渲染方法很难达到这些效果.

一般地说,物体某点到达眼睛的光由发射光和反射光组成.这可以由光传输方程(light transport equation)又称做渲染方程(rendering equation)来表达：

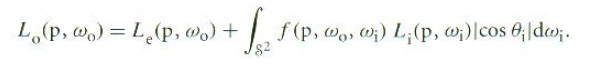
Lo(P, ωo) 是在点P及方向ωo的出射光。
Le(P, ωo) 是在物体自己在点P及方向ωo发出的光。
Li(P, ωi) 是该点在方向ωi入射光。

积分式是指在包含点P的球体上对所有方向的入射光所产生的出射光的贡献值的积分，它用到了BRDF函数和cosine值。

求这个积分的解析值是很困难的，我们必须简化前提或者用数值积分来求解。Whitted的算法忽略了绝大部分方向的入射光线，指对点到光源的方向和全反射和全折射方向上求Li(P, ωi)。换句话说，它把积分转换成对极少数方向上的累加。

我们可以扩展Whitted算法，使其不仅模拟镜面全反射和玻璃。例如，在靠近镜面反射的方向上递归地追踪许多光线，并对它们的结果取平均值，这样我们就得到粗糙表面的反射效果。第14和16章有更详细的解释。当我们递归地追踪光线时，我们就在每个图像点上建立了一颗光线树。从眼睛发出的光线就是这棵树的根。树上每条光线都有一个权值与之联系，这可以让我们模拟那些光滑的但并不100%地反射入射光的表面。

1.2.7 光的传播

前面的讨论假定光在真空中作不衰减地传播，当环境中有雾，烟或灰尘等现象时，就不适用了，而且只要在户外，光线肯定受地球大气的影响。

介质有两种方式影响光的传播。首先，介质可以通过对光的吸收和散射来消弱光的强度。我们可以计算光线原点和交点之间的透射比(transmittance)T来模拟这个效果。另外，介质还可以加强光的强度，比如介质本身发光（火焰等），或者介质从其他的方向传来的光散射到光线的方向去，这就要求体积光线传输方程（见第12章和第17章）。